| Il quinto postulato di Euclide e le geometrie non euclidee
Per una visione completa dell'argomento in questione cliccare sull'allegato file PDF
|
|
Frontespizio e pagina della prima edizione dell ‘ Euclides ab omni naevo vindicatus di Giovanni Gerolamo Saccheri Con quest'opera Saccheri vuole dimostrare che il quinto postulato di Euclide è un teorema in quanto può essere dedotto dai primi quattro postulati e dalle prime 28 proposizioni del primo libro degli elementi. In Nostro espone ragionamenti di un certo rigore logico , ma le conclusioni alle quali perviene non sono corrette . Dalla sostituzione del quinto postulato con altri postulati nasceranno le geometrie non euclidee . |
|
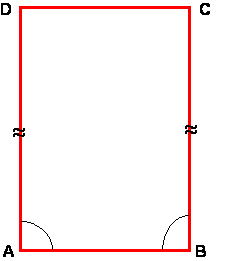
Saccheri non parte dalla negazione del V postulato, ma inizia la sua
dissertazione considerando una figura geometrica che chiama
quadrilatero birettangolo
( oggi chiamato
quadrilatero di Saccheri
) : considera un generico segmento
Saccheri dimostra che essi sono uguali e per quanto riguarda la loro ampiezza ipotizza tre possibilità :
|
|
|
Nokolai Ivanovic Lobacevski Fu il primo matematico a costruire la geometria non euclidea detta iperbolica . Nella predetta geometria iperbolica , la quale non presenta nessuna contraddizione logica , afferma che per un punto di un piano non appartenente ad una retta , è possibile tracciare due distinte “ parallele “ alla retta data . |
|
Gli enti fondamentali
del modello di Klein sono gli stessi
enti della geometria euclidea , che vengono ribattezzati secondo il
seguente schema . Klein
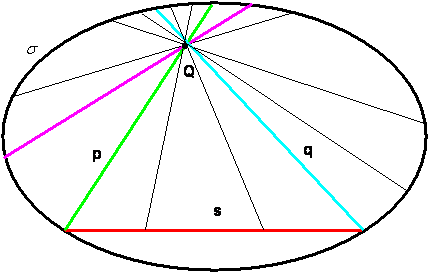
considera una qualsiasi conica , ad esempio l’ellisse
Dal disegno della figura notiamo che tutte le rette passanti per il punto Q si dividono in due classi ciascuna delle quali contiene infinite rette . Una classe contiene le rette con non incontrano la retta s , l’altra contiene le rette che incontrano s in un solo punto . Lobacevski chiama parallele alla retta s condotte dal punto Q le due rette p e q che separano le rette parallele e per Lobacevski il V postulato viene sostituito dal seguente : “ per un punto Q esterno ad una retta s si possono condurre due sole rette parallele ad s “ |
|
|
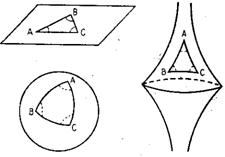
Bernhard Riemann Esente da ogni contraddizione è la geometria ellittica di Riemann nella quale manca la nozione di parallelismo . In tale geometria la somma degli angoli interni di un triangolo è sempre maggiore di due angoli retti .Questa geometria fornì ad Albert Einstein il modello per lo spazio-tempo di Minkowski . |
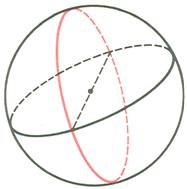 |
Riemann considera come piano una superficie sferica e chiama :
opposti ,cioè gli estremi di un diametro
|
|
Si definisce geodetica la linea che rappresenta la minima distanza tra due punti di una stessa superficie . |
Nella geometria euclidea la somma degli angoli interni di un
triangolo è |
|
Immanuel Kant |
Kant attribuisce allo spazio ed al tempo il carattere di intuizioni a priori . Egli afferma nella Critica della ragion pura quanto segue : << Lo spazio non è un concetto empirico , ricavato da esperienze esterne.........., è una rappresentazione necessaria a priori , la quale serve di fondamento a tutte le intuizioni esterne >> |
|
Karl Friedrich Gauss |
Il grande matematico tedesco , pur essendo convinto che era possibile costruire una geometria diversa da quella costruita da Euclide , non pubblicò i suoi lavori in quanto non voleva ascoltare << le strida dei beoti >> che seguivano acriticamente le concezioni valide in quel periodo . |
|
Isaac Newton |
La fisica classica di Newton considera lo spazio come un contenitore all'interno del quale si trova la materia . Tra lo spazio e la materia contenuta in esso non esiste alcuna interazione . Lo spazio fisico di Newton segue la geometria euclidea ed è cos' definito : << Lo spazio assoluto , per sua natura senza relazione ad alcunché di esterno , rimane sempre uguale ed immobile . |
|
Albert Einstein |
Albert Einstein enuncia la teoria della
relatività generale in base alla quale la presenza della massa dei
corpi incurva lo spazio occupato dalla materia . Le geometrie non
euclidee diventano uno strumento valido per descrivere le
proprietà dello spazio fisico . L'esistenza della deformazione dello spazio prevista da Einstein fu osservata nel 1919 durante un'eclisse totale di Sole . |